Last modified: August 1, 2025

← Back

Big-O Notation

A way of analyzing time it takes for our algorithm to execute as the input size grows.
worst-case runtime

\(O(1)\)

No matter how much our input size grows, the time complexity of O(1) algorithms is always the same.
Most efficient algorithm

# Aray
nums = [1, 2, 3]
nums.append(4)
nums.pop()
nums[0]

# HashMap / Set
hashMap = {}
hashMap["key"] = 10
hashMap.pop("key")

\(O(n)\)

Linear growth scenario
as our input size grows, our time grows proportionally

nums = [1, 2, 3]
sum(nums)
for n in nums:
    print(n)

nums.insert(1, 100)
nums.remove(100)

import heapq
heapq.heapify(nums)

\(O(n^2)\)

Nested loops; two-dimensional arrays

nums = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for i in range(len(nums)):
    for j in range(len(nums[i])):
        print(nums[i][j])

nums = [1, 2, 3]
for i in range(len(nums)):
    for j in range(i+1, len(nums)):
        print(nums[i], nums[j])

# Insertion sort

\(O(n * m)\)

A two-dimensional matrix that's not necessarily a square

nums1, nums2 = [1, 2, 3][4, 5]
for i in range(len(nums1)):
    for j in range(len(nums2)):
        print(nums1[i], nums2[j])

\(O(Log \space n)\)

on every iteration of the loop, we eliminate half of the elements from consideration; we cut array in half until we have nothing remain

given an array of size n, how many times can you cut the value n by two until it equals 1?
\(\rightarrow\) how many times can you take the value 1 and multiply by two until it's equal to n

# binary search
nums = [1, 2, 3, 4, 5]
target = 6
l, r = 0, len(nums) - 1
while l <= r:
    m = (l + r) // 2
    if target < nums[m]
        r = m - 1
    elif target > nums[m]:
        l = m + 1
    else:
        print(m)
        break

# binary search on BST
def search(root, target):
    if not root:
        return False
    if target < root.val:
        return search(root.left, target)
    elif target > root.val:
        return search(root.right, target)
    else:
        return True

\(O(n \space Log \space n)\)

# sort
nums.sort()

# HeapSort
import heapq
nums = [1, 2, 3, 4, 5]
heapq.heapify(nums) # O(N)
while nums:
    heapq.heappop(nums) # O(log n)

# MergeSort
# (and most built-in sorting functions)

\(O(2^n)\)

recursion; Fibonacci recursively

# recursion, tree height n, two branches
def recursion(i, nums):
    if i == len(nums):
        return 0
    branch1 = recursion(i + 1, nums)
    branch2 = recursion(i + 2, nums)

\(O(C^n)\)

# c branches, where c is sometimes n
def recursion(i, nums, c):
    if i == len(nums):
        return 0

    for j in range(i, i + c):
        branch = recursion(j + 1, nums)

\(O(\sqrt n)\)

# Get all factors of n
n = 12
factors = set()
for i in range(1, int(math.sqrt(n)) + 1):
    if n % 1 == 0:
        factors.add(i)
        factors.add(n // i)

\(O(n!)\)

Permutations; traveling salesman problem.
very inefficient

i.e. #46

def permute(self, nums: List[int]) -> List[List[int]]:
    perms = [[]]

    for n in nums:
    new_perms = []
        for p in perms:
            for i in range(len(p)+1):
                p_copy = p.copy()
                p_copy.insert(i, n)
                new_perms.append(p_copy)
        perms = new_perms

    return perms

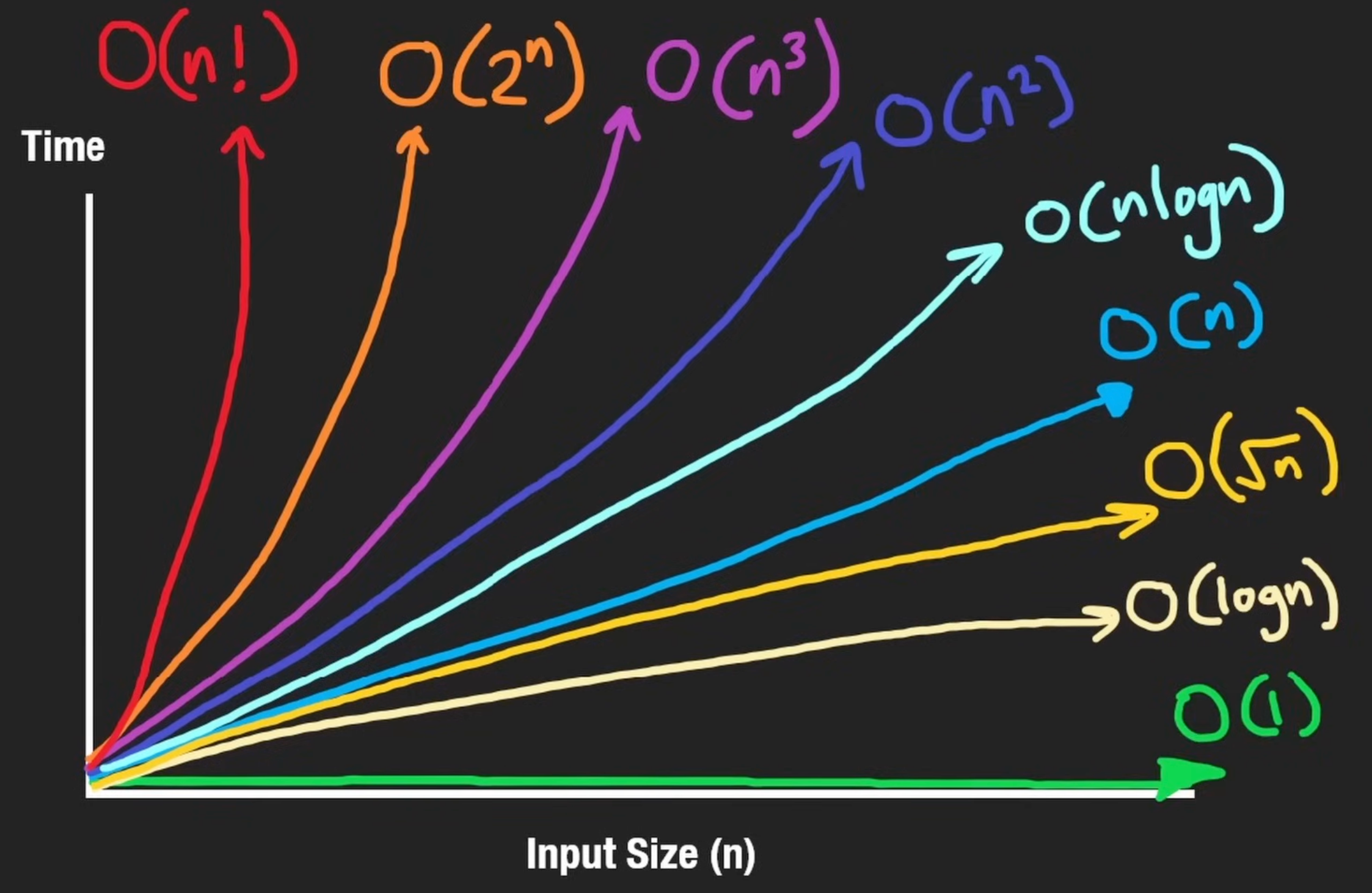
Source: Big-O Notation (NeetCode)